Question

The equiconvex lens has a focal length 'f'. If the lens is cut along the line perpendicular to the principal axis and passing through the pole, what will be the focal length of any half part?

Options

• `"f"/2`

• 2f

• `"3f"/2`

• f

Answer 1

2f

Explanation:

The lens Maker's formula is given as

`1/"f" = (mu_"med" - 1) (1/"R"_1 + 1/"R"_2)`

where, f = focal length of lens,

R₁ = radius of first curved part and

R₂ = Radius of second curved part

As, for equiconvex lens R₁ = R₂ = R (say)

So, `1/"f" = (mu_"real" - 1)2/"R"`    ...(i)

Now, if lens is cut along the line perpendicular to the principal axis as shown in the figure,

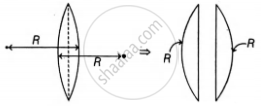
The new cut part of the lens has, R₁ = R and R₂ = ∞
Again by using the lens Maker's formula, focal length of the new part of the lens,

`1/"f'" = (mu_"real" - 1)[1/"R" - (- 1/∞)]`

`=> 1/"f" = (mu_"real" - 1)[1/"R"]`    ...(ii)

So, from the Eqs. (i) and (ii), we get

f' = 2f