Question

The figure shows as triangle AOB and the parabola y = x². The ratio of the area of the triangle AOB to the area of the region AOB of the parabola y = x² is equal to ______.

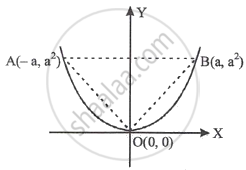
Options

• `3/5`

• `3/4`

• `7/8`

• `5/6`

Answer 1

The figure shows as triangle AOB and the parabola y = x². The ratio of the area of the triangle AOB to the area of the region AOB of the parabola y = x² is equal to `bb(3/4)`.

Explanation:

Area of ΔAOB = `1/2` × 2a × a² = a³ units

Area of region AOB

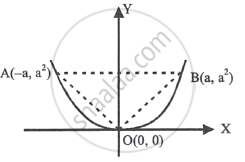
= `2int_0^("a"^2) x  "dy"` = `2int_0^("a"^2) sqrt("y")  "dy"`

= `2["y"^(3//2)/(3//2)]_0^("a"^2)` = `4/3 "a"^3` units

∴ ratio of areas = `"a"^3/(4/3 "a"^3) = 3/4`