Question

The fractional change in the magnetic field intensity at a distance 'r' from centre on the axis of the current-carrying coil of radius 'a' to the magnetic field intensity at the centre of the same coil is ______.

(Take r < a).

Options

• `3/2 r^2/a^2`

• `3/2 a^2/r^2`

• `2/3 a^2/r^2`

• `2/3 r^2/a^2`

Answer 1

The fractional change in the magnetic field intensity at a distance 'r' from centre on the axis of the current-carrying coil of radius 'a' to the magnetic field intensity at the centre of the same coil is `underlinebb(3/2 r^2/a^2)`.

Explanation:

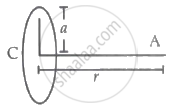
Let the magnetic field intensity at the centre be B_C and at the axis be B_A.

then the fraction change = `(DeltaB)/(B_C) = (B_C - B_A)/(B_A)` .....(i)

at center `B_C = (mu_0I)/(2a)`

at axis `B_A = (mu_0Ia^2)/(2(a^2 + x^2)^{3"/"2})`

Using equation (i) we obtain,

`(DeltaB)/(B_C) = ((mu_0i)/(2a) - (mu_0ia^2)/(2(1^2 + x^2)^{3"/"2}))/((mu_0i)/(2a))`

= `1 - 1/(1 + x^2/a^2)^{3"/"2}`

`(DeltaB)/(B_C) = 1 - (1 + x^2/a^2)^{(-3)/2}`  ....Using binomial (1 + x)ⁿ

= 1 + nx + ........Neglecting higher degree terms as r < a.

`(DeltaB)/(B_C) = 1 - (1 - 3/2 x^2/a^2)`

`(DeltaB)/(B_C) = (3x^2)/(2a^2)` put x = r

`(DeltaB)/(B_C) = (3r^2)/(2a^2)`