Advertisements
Advertisements
Question
The given figure shows an equilateral triangle ABC with each side 15 cm. Also, DE || BC, DF || AC, and EG || AB.
If DE + DF + EG = 20 cm, find FG.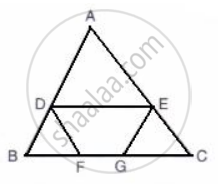
Solution
ABC is an equilateral triangle.
Therefore, AB = BC = AC = 15 cm
∠A = ∠B = ∠C = 60°
In ΔADE, DE || BC ........[ Given ]
∠AED = 60° ........[∵ ∠ACB = 60°]
∠ADE = 60° ........[∵ ∠ACB = 60°]
∠DAE = 180° − (60° + 60°) = 60°
Similarly, BDF and GEC are equilateral triangles.
= 60° .......[∵∠C = 60°]
Let AD = x, AE = x, DE = x ......[∵ ΔADE is an equilateral triangle]
Let BD = y, FD = y, FB = y ......[∵ ΔBDF is an equilateral triangle]
Let EC = z, GC = z , GE = z ...[∵ΔGEC is an equilateral triangle]
Now,
AD + DB = 15 ⇒ x + y = 15 .......(i)
AE + EC = 15 ⇒ x + z = 15 ........(ii)
Given, DE + DF + EG = 20
⇒ x + y + z = 20
⇒ 15 + z = 20 ......[From(i)]
⇒ z = 5
From (ii), we get x = 10
∴ y = 5
Also, BC = 15
BF + FG + GC = 15
⇒ y + FG + z = 15
⇒ 5 + FG + 5 = 15
⇒ FG = 5
