Question

The joint equation of the lines through the origin which forms two of the sides of the equilateral triangle having x = 2 as the third side is ______

Options

• 3y² + x² = 0

• y² + 3x² = 0 

• x² - 3y² = 0 

• y² - 3x² = 0

Answer 1

The joint equation of the lines through the origin forms two of the sides of the equilateral triangle having x = 2 as the third side is x² - 3y² = 0.

Explanation:

 

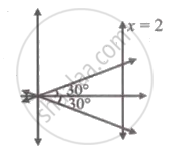
From the diagram, the required lines are

`y = x/sqrt3` i.e., `x - sqrt3y = 0`

and

`y = (-x)/sqrt3` i.e., `x + sqrt3y = 0`

∴ Combined equation is

`(x - sqrt3y)(x + sqrt3y) = 0`

i.e., x² - 3y² = 0