Question

The length of common chord of two intersecting circles is 30 cm. If the diameters of these two circles be 50 cm and 34 cm, calculate the distance between their centres.

Answer 1

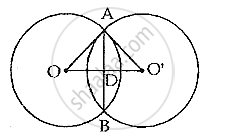
OA = 25 cm and AB = 30 cm

∴ `AD = 1/2× AB =(1/2×30)cm = 15 cm`

Now in right angled ΔADO,

`OA^2 = AD^2 + OD^2`
⇒` OD^2 = OA^2 - OD^2 = 25^2 -15^2`
= 625 - 225 = 400

∴ `OD =sqrt 400 = 20 cm`
Again, we have O 'A = 17 cm
In right angle ΔADO'
` O'A ^2= AD^2 +O'D^2`
⇒ `O'D^2 =O'A^2 - AD^2 = 17^2 -15^2`
⇒ 289 - 225 = 64 
 ∴ O'D 8 cm
∴ OO' (OD+ O'D)
= (20 +8)= 28 cm
∴ the distance between their centres is 28 cm