Question

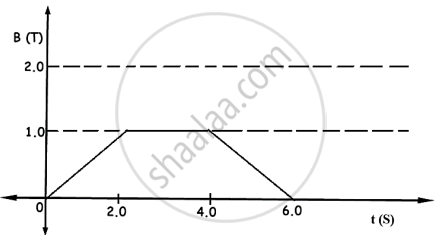
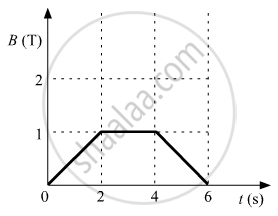
The magnetic field through a circular loop of wire 12 cm in radius and 8.5 Ω resistance, changes with time as shown in the figure. The magnetic field is perpendicular to the plane of the loop. Calculate the induced current in the loop and plot it as a function of time.

Answer 1

Area of the circular loop = πr²

= 3.14 × (0.12)² m² = 4.5 × 10^-2 m²

E = `- ("d"phi)/"dt" = - "d"/"dt" ("BA") = - "A"  "dB"/"dt" = - "A" * ("B"_2 - "B"_1)/("t"_2 - "t"_1)`

For 0 < t < 2s

E₁ = - 4.5 × 10^-2 × `{(1 - 0)/(2 - 0)}`

`= - 2.25 xx 10^-2`V

`therefore "I"_1 = "E"_1/"R"`

`= (- 2.25 xx 10^-2)/8.5`A

`= - 2.6 xx 10^-3`A

= - 2.6 mA

For 2s < t < 4s,

`"E"_2 = - 4.5 xx 10^-2 xx {(1 - 1)/(4 - 2)}` = 0

`therefore "I"_2 = "E"_2/"R" = 0`

For 4s < t < 6s,

`"I"_3 = - (4.5 xx 10^-2)/8.5 xx {(0 - 1)/(6 - 4)}`A

= 2.6 mA

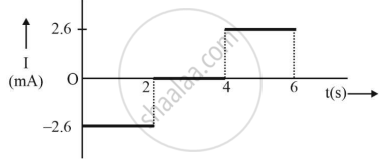
	0 < t < 2s	2 < t < 4s	4 < t < 6s
E(V)	- 0.023	0	+ 0.023
I(mA)	- 2.6	0	+ 2.6