Question

The magnitude of vectors `vec"A"`, `vec"B"` and `vec"C"` are respectively 12, 5 and 13 units and `vec"A"` + `vec"B"` =  `vec"C"`, then the angle between `vec"A"` and `vec"B"` is ______.

Options

• 0

• π

• `pi/2`

• `pi/4`

Answer 1

The magnitude of vectors `vec"A"`, `vec"B"` and `vec"C"` are respectively 12, 5 and 13 units and `vec"A"` + `vec"B"` =  `vec"C"`, then the angle between `vec"A"` and `vec"B"` is `underlinebb(pi/2)`.

Explanation:

The Vectors `vec"A", vec"B"  "and"  vec"C"` can be represented as shown in figure.

 

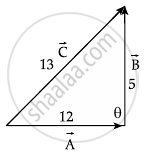
`|vecA + vecB| = |vecC|`

⇒ `|vecC| = sqrt(|vecA|^2 + |vecB|^2 + 2|vecA||vecB|costheta)`

⇒ 13 = `sqrt(12^2 + 5^2 + 2 xx 12 xx 5costheta)`

⇒ 169 = 169 + 120 cosθ

⇒ cosθ = 0

⇒ `theta = pi/2`

Clearly angle between `vec"A"  "and"  vec"B"  "is"  pi/2`.