Question

The maximum area of a right angled triangle with hypotenuse h is:

Options

• `h^2/(2sqrt(2)`

• `h^2/2`

• `h^2/sqrt(2)`

• `h^2/2`

Answer 1

`h^2/2`

Explanation:

Given that the hypotenuse of right-angled triangle is h.

Let base = b

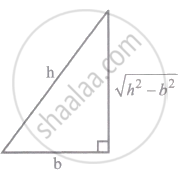
Altitude or (perpendicular) = `sqrt(h^2 - b^2)`

Area of triangle = `1/2` base × altitude

= `1/2 xx b xx sqrt(h^2 - b^2)`

⇒ `(dA)/(db) = 1/2 [sqrt(h^2 - b^2) + b xx (-2b)/(2sqrt(h^2 - b^2))]`

= `1/2 [sqrt(h^2 - b^2) - b^2/sqrt(h^2 - b^2)]`

= `1/2 ([h^2 - 2b^2])/sqrt(h^2 - b^2)`

For maximum area, `(dA)/(db)` = 0

⇒ `1/2 ([h^2 - 2b^2])/sqrt(h^2 - b^2)` = 0

⇒ `[h^2 - 2b^2]` = 0

⇒ `h^2 = 2b^2` = 0

⇒ `b = h/sqrt(2)`

A = `1/2 xx b xx sqrt(h^2 - b^2)`

= `1/2 xx h/sqrt(2) xx sqrt(h^2 - h^2/2)`

= `h^2/4`