Advertisements
Advertisements
Question
The maximum frequency for reflection of sky waves from a certain layer of the ionosphere is found to be fmax = 9(Nmax)1/2, where Nmax is the maximum electron density at that layer of the ionosphere. On a certain day, it is observed that signals of frequencies higher than 5 MHz are not received by reflection from the F1 layer of the ionosphere while signals of frequencies higher than 8 MHz are not received by reflection from the F2 layer of the ionosphere. Estimate the maximum electron densities of the F1 and F2 layers on that day.
Solution
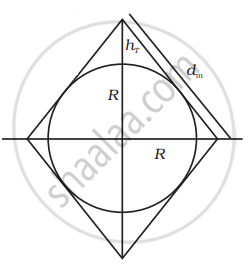
`d_m^2 = 2(R + h_T)^2`
`8Rh_T = 2(R + h_T)^2` ......(∵ `dm = 2sqrt(2Rh_T))`
`4Rh_T = R^2 + h_T^2 + 2Rh_T`
`(R - h_T)^2` = 0
`R = h_T`
Since space wave frequency is used, λ << hT, hence only tower height is taken into consideration. In three dimensions, 6 antenna towers of hT = R would do.
RELATED QUESTIONS
Is it necessary for a transmitting antenna to be at the same height as that of the receiving antenna for line-of-sight communication? A TV transmitting antenna is 81m tall. How much service area can it cover if the receiving antenna is at the ground level?
Name the three different modes of propagation in a communication system. State briefly why do the electromagnetic waves with a frequency range from a few MHz up to 30 MHz can reflect back to the earth. What happens when the frequency range exceeds this limit?
What do you mean by skip distance?
The wavelength of electromagnetic wave employed in space communication very over a range of
The radio wave of frequency 300 MHz to 3000 MHz be.long to
An antenna is
The Q of a resonant transmission line is
The component of the ground wave attenuated by conducting earth is ______.
Three waves A, B and C of frequencies 1600 kHz, 5 MHz and 60 MHz, respectively are to be transmitted from one place to another. Which of the following is the most appropriate mode of communication ______.
(i) The intensity of a light pulse travelling along a communication channel decreases exponentially with distance x according to the relation I = Ioe–αx, where Io is the intensity at x = 0 and α is the attenuation constant. Show that the intensity reduces by 75 per cent after a distance of `((In 4)/α)`
(ii) Attenuation of a signal can be expressed in decibel (dB) according to the relation dB = `10 log_10 (I/I_0)`. What is the attenuation in dB/km for an optical fibre in which the intensity falls by 50 per cent over a distance of 50 km?
