Question

The maximum value of z = 9x + 11y subject to 3x + 2y ≤ 12, 2x + 3y ≤ 12, x ≥ 0, y ≥ 0 is _______.

Options

• 44

• 54

• 36

• 48

Answer 1

The maximum value of z = 9x + 11y subject to 3x + 2y ≤ 12, 2x + 3y ≤ 12, x ≥ 0, y ≥ 0 is 48.

Explanation:

We have, Z = 9x + 11y

Subject to 3x + 2y ≤ 12, 2x + 3y ≤ 12

On taking given constraints as equation, we get the following graph.

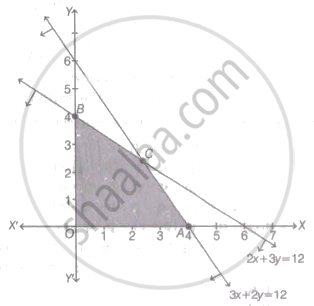
Intersection point of lines 3x + 2y = 12 and 2x + 3y = 12 is C `(12/5, 12/5)`.

Here, OACBO is the feasible region whose corner points are O(0,0), A(4, 0), C`(12/5, 12/5)` and B (0, 4)

Corner points	Z = 9x + 11y
O(0, 0)	0 + 0 = 0
A(4, 0)	9 × 4 + 11 × 0 = 36
B(0, 4)	9 × 0 + 11 × 4 = 44
C`(12/5, 12/5)`	`9 xx 12/5 + 11 xx 12/5 = 48` (maximum)