Advertisements
Advertisements
Question
The maximum value of Z = 4x + 3y subjected to the constraints 3x + 2y ≥ 160, 5x + 2y ≥ 200, x + 2y ≥ 80; x, y ≥ 0 is
Options
320
300
230
none of these
Solution
none of these
We need to maximize the function Z = 4x + 3y
Converting the given inequations into equations, we obtain
Region represented by 3x + 2y ≥ 160:
The line 3x + 2y = 160 meets the coordinate axes at \[A\left( \frac{160}{3}, 0 \right)\] and B(0, 80) respectively. By joining these points we obtain the line 3x + 2y = 160.Clearly (0,0) does not satisfies the inequation 3x + 2y ≥ 160. So,the region in xy plane which does not contain the origin represents the solution set of the inequation 3x + 2y ≥ 160.
Region represented by 5x +2y ≥ 200 :
The line 5x +2y = 200 meets the coordinate axes at C(40,0) and D(0, 100) respectively. By joining these points we obtain the line 5x +2y = 200.Clearly (0,0) does not satisfies the inequation 5x +2y ≥ 200. So,the region which does not contain the origin represents the solution set of the inequation 5x +2y ≥ 200.
Region represented by x +2y ≥ 80:
The line x +2y = 80 meets the coordinate axes at E(80,0) and F(0, 40) respectively. By joining these points we obtain the line x +2y = 80.Clearly (0,0) does not satisfies the inequation x +2y ≥ 80. So,the region which does not contain the origin represents the solution set of the inequation x+2y ≥ 80.
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 3x + 2y ≥ 160, 5x +2y ≥ 200, x +2y ≥ 80, x ≥ 0, and y ≥ 0 are as follows.
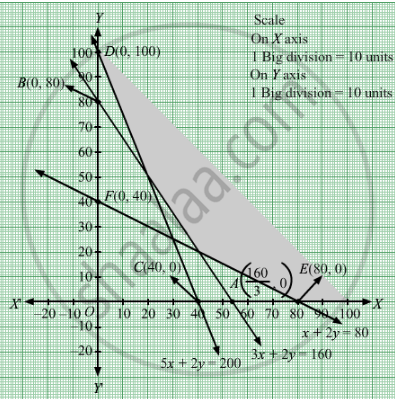
Here, we see that the feasible region is unbounded. Therefore,maximum value is infinity.
APPEARS IN
RELATED QUESTIONS
A rubber company is engaged in producing three types of tyres A, B and C. Each type requires processing in two plants, Plant I and Plant II. The capacities of the two plants, in number of tyres per day, are as follows:
| Plant | A | B | C |
| I | 50 | 100 | 100 |
| II | 60 | 60 | 200 |
The monthly demand for tyre A, B and C is 2500, 3000 and 7000 respectively. If plant I costs Rs 2500 per day, and plant II costs Rs 3500 per day to operate, how many days should each be run per month to minimize cost while meeting the demand? Formulate the problem as LPP.
Vitamins A and B are found in two different foods F1 and F2. One unit of food F1contains 2 units of vitamin A and 3 units of vitamin B. One unit of food F2 contains 4 units of vitamin A and 2 units of vitamin B. One unit of food F1 and F2 cost Rs 50 and 25 respectively. The minimum daily requirements for a person of vitamin A and B is 40 and 50 units respectively. Assuming that any thing in excess of daily minimum requirement of vitamin A and B is not harmful, find out the optimum mixture of food F1 and F2 at the minimum cost which meets the daily minimum requirement of vitamin A and B. Formulate this as a LPP.
A firm manufactures two products, each of which must be processed through two departments, 1 and 2. The hourly requirements per unit for each product in each department, the weekly capacities in each department, selling price per unit, labour cost per unit, and raw material cost per unit are summarized as follows:
| Product A | Product B | Weekly capacity | |
| Department 1 | 3 | 2 | 130 |
| Department 2 | 4 | 6 | 260 |
| Selling price per unit | Rs 25 | Rs 30 | |
| Labour cost per unit | Rs 16 | Rs 20 | |
| Raw material cost per unit | Rs 4 | Rs 4 |
The problem is to determine the number of units to produce each product so as to maximize total contribution to profit. Formulate this as a LPP.
A firm has to transport at least 1200 packages daily using large vans which carry 200 packages each and small vans which can take 80 packages each. The cost of engaging each large van is ₹400 and each small van is ₹200. Not more than ₹3000 is to be spent daily on the job and the number of large vans cannot exceed the number of small vans. Formulate this problem as a LPP given that the objective is to minimize cost
The solution set of the inequation 2x + y > 5 is
Objective function of a LPP is
Which of the following sets are convex?
Consider a LPP given by
Minimum Z = 6x + 10y
Subjected to x ≥ 6; y ≥ 2; 2x + y ≥ 10; x, y ≥ 0
Redundant constraints in this LPP are
The objective function Z = 4x + 3y can be maximised subjected to the constraints 3x + 4y ≤ 24, 8x + 6y ≤ 48, x ≤ 5, y ≤ 6; x, y ≥ 0
If the constraints in a linear programming problem are changed
Which of the following is not a convex set?
A company manufactures two types of toys A and B. A toy of type A requires 5 minutes for cutting and 10 minutes for assembling. A toy of type B requires 8 minutes for cutting and 8 minutes for assembling. There are 3 hours available for cutting and 4 hours available for assembling the toys in a day. The profit is ₹ 50 each on a toy of type A and ₹ 60 each on a toy of type B. How many toys of each type should the company manufacture in a day to maximize the profit? Use linear programming to find the solution.
Choose the correct alternative:
The constraint that in a college there are more scholarship holders in FYJC class (X) than in SYJC class (Y) is given by
Choose the correct alternative:
How does a constraint, “A washing machine can hold up to 8 kilograms of cloths (X)” can be given?
State whether the following statement is True or False:
The half-plane represented by 3x + 4y ≥ 12 includes the point (4, 3)
Tyco Cycles Ltd manufactures bicycles (x) and tricycles (y). The profit earned from the sales of each bicycle and a tricycle are ₹ 400 and ₹ 200 respectively, then the total profit earned by the manufacturer will be given as ______
By spending almost ₹ 250, Rakhi bought some kg grapes (x) and some dozens of bananas (y), then as a constraint this information can be expressed by ______
A doctor prescribed 2 types of vitamin tablets, T1 and T2 for Mr. Dhawan. The tablet T1 contains 400 units of vitamin and T2 contains 250 units of vitamin. If his requirement of vitamin is at least 4000 units, then the inequation for his requirement will be ______
Ms. Mohana want to invest at least ₹ 55000 in Mutual funds and fixed deposits. Mathematically this information can be written as ______
Determine the minimum value of Z = 3x + 2y (if any), if the feasible region for an LPP is shown in Figue.
Solve the following LPP graphically:
Maximise Z = 2x + 3y, subject to x + y ≤ 4, x ≥ 0, y ≥ 0
Minimise Z = 3x + 5y subject to the constraints:
x + 2y ≥ 10
x + y ≥ 6
3x + y ≥ 8
x, y ≥ 0
The corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5), (15, 15), (0, 20). Let Z = px + qy, where p, q > 0. Condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20) is ______.
The common region determined by all the linear constraints of a LPP is called the ______ region.
In maximization problem, optimal solution occurring at corner point yields the ____________.
A type of problems which seek to maximise (or, minimise) profit (or cost) form a general class of problems called.
Conditions under which the object function is to be maximum or minimum are called ______.
