Question

The minimum value of α for which the equation `4/sinx + 1/(1 - sinx)` = α has at least one solution in `(0, π/2)` is ______.

Options

• 7

• 8

• 9

• 10

Answer 1

The minimum value of α for which the equation `4/sinx + 1/(1 - sinx)` = α has at least one solution in `(0, π/2)` is 9.

Explanation:

f(x) = `4/sinx + 1/(1 - sinx)`

Let sinx = t

`0 < x < π/2`

⇒ 0 < t < 1

f(t) = `4/"t" + 1/(1 - "t")`

f'(t) = `(-4)/"t"^2 + 1/(1 - "t")^2`

= `("t"^2 - 4(1 - "t")^2)/("t"^2(1 - "t")^2`

= `(("t" - 2(1 - "t"))("t" + 2(1 - "t")))/("t"^2(1 - "t")^2`

f'(t) = `((3"t" - 2)(2 - "t"))/("t"^2(1 - "t")^2`

Find the sign scheme of f'(t)

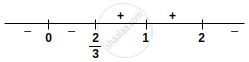
Minimum of f occurs at the point where f changes its sign from negative to positive.

f is minimum at t = `2/3`

∴ α_min = `f(2/3) = 4/(2/3) + 1/(1 - 2/3)` = 6 + 3 = 9