Advertisements
Advertisements
Question
The number of sides of a regular polygon where each exterior angle has a measure of 45° is ______.
Options
8
10
4
6
Solution
The number of sides of a regular polygon where each exterior angle has a measure of 45° is 8.
Explanation:
We know that, the sum of exterior angles taken in an order of a polygon is 360°.
Since, each exterior angle measures 45°,
Therefore the number of sides
= `"Sum of exterior angles"/"Measure of an exterior angle"`
= `360^circ/45^circ`
= 8
APPEARS IN
RELATED QUESTIONS

Which of the following is not true for an exterior angle of a regular polygon with n sides?
The measure of each exterior angle of a regular polygon of 18 sides is ______.
The number of sides of a regular polygon, where each exterior angle has a measure of 36°, is ______.
The sum of all exterior angles of a polygon is ______.
Triangle is a polygon whose sum of exterior angles is double the sum of interior angles.
The sum of interior angles and the sum of exterior angles taken in an order are equal in case of quadrilaterals only.
The interior angles of a triangle are in the ratio 1:2:3, then the ratio of its exterior angles is 3:2:1.
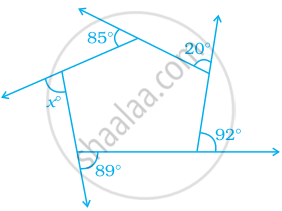
In the figure, find the value of x.