Question

The object function z = 4x₁ + 5x₂, subject to 2x₁ + x₂ ≥ 7, 2x₁ + 3x₂ ≤ 15, x₂ ≤ 3, x₁, x₂ ≥ 0 has minimum value at the point is ______.

Options

• on X-axis

• on Y-axis

• at the origin

• on the line parallel to X-axis

Answer 1

The object function z = 4x₁ + 5x₂, subject to 2x₁ + x₂ ≥ 7, 2x₁ + 3x₂ ≤ 15, x₂ ≤ 3, x₁, x₂ ≥ 0 has minimum value at the point is on X-axis.

Explanation:

The objective function is given as, minimize, z = 4x₁ + 5x₂

Subject to constraints, 2x₁ + x₂ ≥ 7, 2x₁ + 3x₂ ≤ 15, x₂ ≤ 3 and x₁, x₂ ≥ 0

For line 2x₁ + x₂ = 7

x1	0	1	2	3
x2	7	5	3	1

For line 2x₁ + 3x₂ = 15

x1	0	3	6
x2	5	3	1

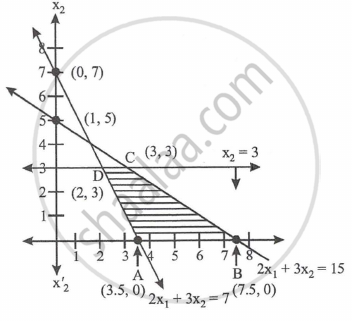
Now, the value of z at comer points are calculated as:

Corner points	z = 4x1 + 5x2
A(3.5, 0)	z = 4 × 3.5 + 5 × 0 = 14 (minimum)
B(7.5, 0)	z = 4 × 7.5 + 5 × 0 = 30
C(3, 3)	z = 4 × 3 + 5 × 3 = 27
D(2, 3)	z = 4 × 2 + 5 × 3 = 23

Hence, the minimum value of z is 14 at point (3.5, 0) which lies on X-axis.