Question

The objective function Z = x₁ + x₂, subject to the constraints are x₁ + x₂ ≤ 10, – 2x₁ + 3x₂ ≤ 15, x₁ ≤ 6, x₁, x₂ ≥ 0, has maximum value ______ of the feasible region.

Options

• at only one point

• at only two points

• at every point of the segment joining two points

• at every point of the line joining two points equivalent to

Answer 1

The objective function Z = x₁ + x₂, subject to the constraints are x₁ + x₂ ≤ 10, – 2x₁ + 3x₂ ≤ 15, x₁ ≤ 6, x₁, x₂ ≥ 0, has maximum value at every point of the segment joining two points of the feasible region.

Explanation:

Since, objective function is Z = x₁ + x₂ and given constraints are

x₁ + x₂ ≤ 10, – 2x₁ + 3x₂ ≤ 15, x₁ ≤ 6, x₁, x₂ ≥ 0

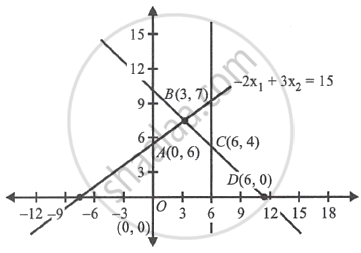
Now, the point of intersection oflines x₁ + x₂ = 10 and – 2x₁ + 3x₂ = 15 is B(3, 7) and point of intersection of lines x₁ = 6 and x₁ + x₂ = 10 is C(6, 4)

Here, the feasible region is OABCD. The corner points of the feasible region are O(0, 0), A(0, 6), B(3, 7), C(6, 4) and D(6, 0).

At O(0, 0)	Z = 0 + 0 = 0
At A(0,6)	Z = 0 + 6 = 6
At B(3,7)	Z = 3 + 7 = 10
At C(6,4)	Z = 6 + 4 = 10
At D(6,0)	Z = 6 + 0 = 6

Hence, Z is maximum at each point of the segment joining two points B(3, 7) and C(6, 4)