Advertisements
Advertisements
Question
The path of a train A is given by the equation 3x + 4y − 12 = 0 and the path of another train B is given by the equation 6x + 8y − 48 = 0. Represent this situation graphically.
Solution
The paths of two trains are given by the following pair of linear equations.
3x + 4y - 12 = 0 ...(1)
6x + 8y - 48 = 0 ...(2)
In order to represent the above pair of linear equations graphically. We need two points on the line representing each equation. That is, we find two solutions of each equation as given below:
We have
3x + 4y - 12 = 0
Putting y = 0, we get
`3x + 4 xx 0 - 12 = 0`
`=> 3x = 12`
`=> x = 12/3 = 4`
Putting x = 0, we get
`3 xx 0 + 4y - 12 = .0`
=> 4y = 12
`=> y = 12/4 = 3`
Thus, two solution of equation 3x + 4y - 12 = 0 are (0.3) and (4,0)
We have
6x + 8y - 48 = 0
Putting x = 0 we get
`6 xx 0 + 8y - 48 = 0
`=> 8y = 48`
`=> y = 48/8`
`=> = 6`
Putting y = 0 we get
`6x + 8 xx 0 = 48 = 0`
`=> 6x = 48`
`=> x = 48/6 = 8`
Thus, two solution of equation 6x + 8y - 48 = 0 are (0, 6) and (8,0)
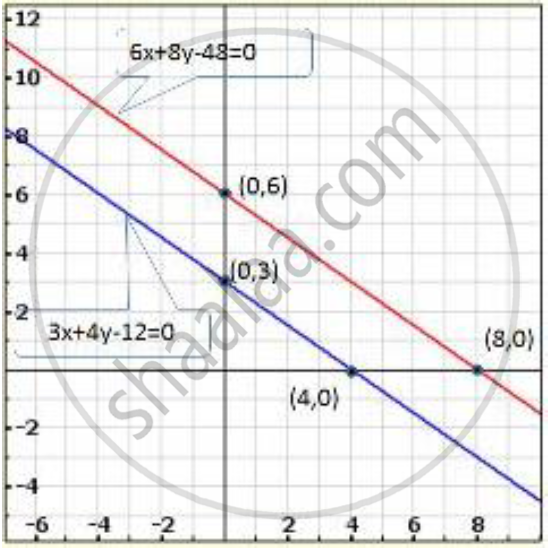
Clearly, two lines intersect at (-1, 2)
Hence, x = -1, y = 2 is the solution of the given system of equations.
