Advertisements
Advertisements
Question
The perimeter of an arc of radius 4.2 cm is 12.8 cm. Determine the angle subtended by the arc at the centre of circle.
Solution
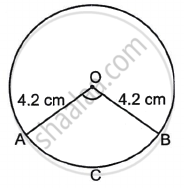
Given: Radius of arc = 4.2 cm and perimeter of arc = 12.8 cm.
Consider the sector OACB,
Length of the arc ABC = `θ/360^circ xx 2 πr` ......(i)
Perimeter of the sector OACB = OA + arc ACB + OB
= `r + θ/360 xx 2πr + r`
= `2r + θ/360 xx 2πr`
Thus, the perimeter of the arc = `2r + θ/360 xx 2πr`
According to the question,
`2r + θ/360 xx 2πr` = 12.8 ......(ii)
Substituting the value of r in equation (ii),
`2 xx 4.2 + θ/360 xx 2π xx 4.2` = 12.8
`8.4 + θ/360 xx 2π xx 4.2` = 12.8
`θ/360 xx 2π xx 4.2` = 12.8 – 8.4
`θ/360 xx 2 xx 22/7 xx 4.2` = 4.4
`θ/360 xx 2 xx 22 xx 0.6` = 4.4
θ = `(4.4 xx 360)/(22 xx 0.6 xx 2)` = 60°
As a result, the circle's center's arc subtends a 60° angle.
APPEARS IN
RELATED QUESTIONS
The radius of a circle is 10 cm. The measure of an arc of the circle is 54°. Find the area of the sector associated with the arc. (\[\pi\]= 3.14 )
The measure of an arc of a circle is 80° and its radius is 18 cm. Find the length of the arc. (π = 3.14)
Area of a sector of a circle of radius 15 cm is 30 cm2 . Find the length of the arc of the sector.
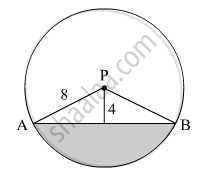
In the given figure, seg AB is a chord of a circle with centre P. If PA = 8 cm and distance of chord AB from the centre P is 4 cm, find the area of the shaded portion. ( \[\pi\] = 3.14, \[\sqrt{3}\]= 1.73 )

In the given figure, square ABCD is inscribed in the sector A - PCQ. The radius of sector C - BXD is 20 cm. Complete the following activity to find the area of shaded region
In Δ ABC, if ∠ A = 65° ; ∠ B = 40° then find the measure of ∠ C.
Length of a rectangular tank is twice its breadth. If the
depth of the tank is 3 m and area of its four walls is 108 m2, find the
length of the tank.
Find the length of an arc if measure of the arc is 90° and its radius
is 14 cm.
Measure of an arc of a sector of a circle is 900 and its radius is 7cm. Find the perimeter of the sector.
(A) 44 cm (B) 25 cm (C) 36 cm (D) 56 cm
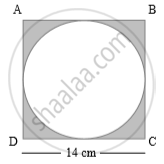
A circle is inscribed in square ABCD of side 14 cm. Complete the following activity to find the area of the shaded portion.
Activity:
Area of square ABCD = ______
= 142
= 196 cm2
Area of circle = πr2 = `22/7xx 7^2`
= ____ cm2
Area of shaded portion = Area of square ABCD – Area of circle
= 196 – _______
= _____ cm2
Match the following:
| Column A | Column B |
| (i) Area of a circle | (a) `1/4 pi"r"^2` |
| (ii) Circumference of a circle | (b) (π + 2)r |
| (iii) Area of the sector of a circle | (c) πr2 |
| (iv) Circumference of a semicircle | (d) 2πr |
| (v) Area of a quadrant of a circle | (e) `theta^circ/360^circ xx pi"r"^2` |
For the sectors with given measures, find the length of the arc, area and perimeter. (π = 3.14)
central angle 45°, r = 16 cm
For the sectors with given measures, find the length of the arc, area and perimeter. (π = 3.14)
central angle 120°, d = 12.6 cm
Two gates are fitted at the entrance of a library. To open the gates easily, a wheel is fixed at 6 feet distance from the wall to which the gate is fixed. If one of the gates is opened to 90°, find the distance moved by the wheel (π = 3.14)
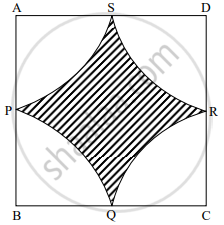
In the given figure `square`ABCD is a square of side 50 m. Points P, Q, R, S are midpoints of side AB, side BC, side CD, side AD respectively. Find area of shaded region
If x = `θ/360` × 2πr then what is x in the formula?
