Advertisements
Advertisements
Question
The product of the two numbers is 528. If the product of their unit’s digits is 8 and the product of their ten’s digits is 4; find the numbers.
Solution
The unit digits of the numbers must satisfy a × b = 8.
The possible pairs for the unit digits (a, b) are:
(1, 8), (2, 4), (4, 2), (8, 1)
The tens digits of the numbers must satisfy: x × y = 4.
The possible pairs for the tens digits (x, y) are:
(1, 4), (2, 2), (4, 1).
Form the possible numbers using the tens and unit digit combinations and calculate their product to match 528
Check combinations:
- 12 × 44 = 528
- 44 × 12 = 528
Verify
- The unit digits 2 × 4 = 82 (satisfied).
- The tens digits 1 × 4 = 41 (satisfied).
The two numbers are: 12 and 44.
APPEARS IN
RELATED QUESTIONS
Is a + b + c = a + (b + c) = (b + a) + c ?
Which property of addition is satisfied by :
(7 + 6) x 10 = 7 x 10 + 6 x 10
State True or False:
The sum of two odd numbers is an even number
Write the identify number, if possible for subtraction.
Evaluate using properties :
548 x 98
Evaluate using properties :
924 x 988
Evaluate using properties :
55873 x 94 + 55873 x 6
Evaluate using properties :
333 x 987 + 13 x 3333
Complete the following magic squares:
| 4 | _______ | 8 |
| _______ | 7 | ________ |
| _______ | _______ | 10 |
See the following pattern carefully:
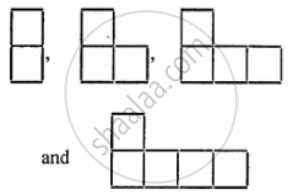
- If n denotes the number of figures and S denotes the number of matches; find S in terms of n.
- Find how many matches are required to make the :
(1) 15th figure
(2) 40th figure - Write a discretion of the pattern in words.
