Advertisements
Advertisements
Question
The radii of curvature of a lens are + 20 cm and + 30 cm. The material of the lens has a refracting index 1.6. Find the focal length of the lens (a) if it is placed in air, and (b) if it is placed in water (μ = 1.33).
Solution
Given,
Radii of curvature of a lens, (R1) = +20 cm and R2 = +30 cm
Refractive index of the material of the lens, (μ) = 1.6
Refractive index of water, (μwater) = 1.33
(a)
When the lens is placed in air,
Using lens maker formula: \[\frac{1}{f} = (\mu - 1)\left[ \frac{1}{R_1} - \frac{1}{R_2} \right]\]
\[\frac{1}{f} = 0 . 6\left[ \frac{1}{20} - \frac{1}{30} \right]\]
\[f = \frac{0 . 6}{1060 \times 10}\]
f = 100 cm
Thus, the focal length of the lens is 100 cm when it is placed in air.
(b)When the lens is placed in water
\[\frac{1}{f} = \left[ \frac{\mu_{lens}}{\mu_{water}} - 1 \right]\left[ \frac{1}{R_1} - \frac{1}{R_2} \right]\]
\[= \left( \frac{1 . 60}{1 . 33} - 1 \right)\left[ \frac{1}{60} \right]\]
\[= \frac{28}{133 \times 60} \simeq \frac{1}{300}\]
\[\Rightarrow\] f = 300 cm.
Thus, the focal length of the lens is 300 cm when it is placed in water.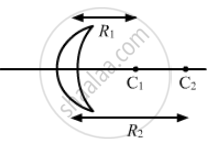
APPEARS IN
RELATED QUESTIONS
A converging lens is kept coaxially in contact with a diverging lens – both the lenses being of equal focal length. What is the focal length of the combination?
Two thin convex lenses L1 and L2 of focal lengths f1 and f2, respectively, are placed coaxially in contact. An object is placed at a point beyond the focus of lens L1. Draw a ray diagram to show the image formation by the combination and hence derive the expression for the focal length of the combined system.
A convex lens is placed in contact with a plane mirror. A point object at a distance of 20 cm on the axis of this combination has its image coinciding with itself. What is the focal length of the lens?
When two thin lenses are kept in contact, prove that their combined or effective focal length F is
given by :
`1/F = 1/f_1 + 1/f_2`
where the terms have their usual meaning.
A convex lens of focal length f1 is kept in contact with a concave lens of focal length f2. Find the focal length of the combination.
A single lens is mounted in a tube. A parallel beam enters the tube and emerges out of the tube as a divergent beam. Can you say with certainty that there is a diverging lens in the tube?
An air bubble is formed inside water. Does it act as a converging lens or a diverging lens?
A thin lens made of a material of refractive index μ2 has a medium of refractive index μ1on one side and a medium of refractive index μ3 on the other side. The lens is biconvex and the two radii of curvature have equal magnitude R. A beam of light travelling parallel to the principal axis is incident on the lens. Where will the image be formed if the beam is incident from (a) the medium μ1 and (b) from the medium μ3?
A point object is placed on the principal axis of a convex lens (f = 15 cm) at a distance of 30 cm from it. A glass plate (μ = 1.50) of thickness 1 cm is placed on the other side of the lens perpendicular to the axis. Locate the image of the point object.
Two thin lenses are in contact and the focal length of the combination is 80 cm. If the focal length of one lens is 20 cm, then the power of the other lens will be:
A concave and convex lens have the same focal length of 20 cm and are placed in contact to form a lens combination. The combination is used to view an object of 5 cm length kept at 20 cm from the lens combination. As compared to the object, the image will be
