Question

The resultant `vec"R"` of `vec"P"` and `vec"Q"` is perpendicular to `vec"P"`. Also `|vec"P"|=|vec"R"|`. The angle between `vec"P"` and `vec"Q"` is ______.
[tan 45° = 1]

Options

• `(5pi)/4`

• `(7pi)/4`

• `(pi)/4`

• `(3pi)/4`

Answer 1

The resultant `vec"R"` of `vec"P"` and `vec"Q"` is perpendicular to `vec"P"`. Also `|vec"P"|=|vec"R"|`. The angle between `vec"P"` and `vec"Q"` is `underlinebb((3pi)/4)`.

Explanation:

Given that R is resultant of `vec"P"` and `vec"Q"` as shown in the figure below,

BC = P, CA = Q and BA = R

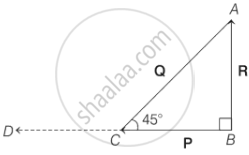
Given, BA and BC are perpendicular and equal in magnitude. So, from property of triangle,

∠ACB = 45°

Now, BC has to be extended up to D so,

that CD = P

Now, CD and CA have the initial point C, so the angle between CD and CA;

= 180° - 45° = 135° = `(3pi)/4`

So, angle between `vec"P"` and `vec"Q"` is `(3pi)/4`.