Question

The shadow of a tower standing on a level ground is found to be 40 m longer when the Sun's altitude is 30° than when it was 60°. Find the height of the tower and the length of original shadow. (use `sqrt3` = 1.73)

Answer 1

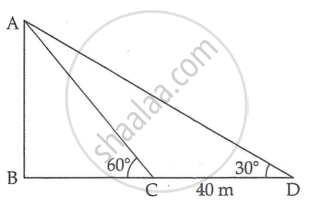
Let AB be the tower

From the given conditions,

CD = 40 m      ...[Given]

Let BC = x m

And Height of tower AB be h m

Now,

In `triangle`ABC,

⇒ tan 60° = `(AB)/(BC)`

⇒ tan 60° = `h/x`

⇒ `sqrt3 = h/x`

⇒ h = `sqrt3x`      ...(i)

 In `triangle`ABD,

⇒ tan 30° = `(AB)/(BD)`

⇒ `1/sqrt3 = h/((x + 40))`

⇒ x + 40 = `sqrt3h`

⇒ x + 40 = `sqrt3(sqrt3x)`      ...[from (i)]

⇒ x + 40 = 3x

⇒ 2x = 40

⇒ x = 20 m

So, h = 20`sqrt3` m

Hence,

Height of tower = 20`sqrt3` m

Length of original shadow = 20 m