Question

The shadow of a tower standing on a level plane is found to be 50 m longer when Sun’s elevation is 30° than when it is 60°. Then the height of the tower is ____________.

Options

• `20 sqrt3`

• `25 sqrt3`

• `10 sqrt3`

• `30 sqrt3`

Answer 1

The shadow of a tower standing on a level plane is found to be 50 m longer when Sun’s elevation is 30° than when it is 60°. Then the height of the tower is `underline(25 sqrt3)`.

Explanation:

Given condition can be represented as follows where SQ is the pole.

Let the height be h and RQ = x m

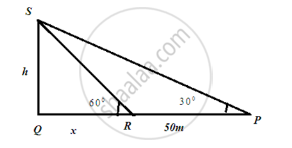
Then from the figure,

`"tan"  60^circ = "SQ"/"RQ"`

`=> sqrt3 = "h"/"x"`

`=> "x" = "h"/sqrt3`

`"tan"  30^circ = "SQ"/"PQ"`

`=> 1/sqrt3 = "h"/(50 + "x")`

`=> 1/sqrt3 = "h"/(50 + "h"/sqrt3)`

`=> 1/sqrt3 (50 + "h"/sqrt3) = "h"`

`=> 50/sqrt2 + "h"/3 = "h"`

`=> 50/sqrt3 = (2"h")/3`

`=> "h" = 25 sqrt3  "m"`