Advertisements
Advertisements
Question
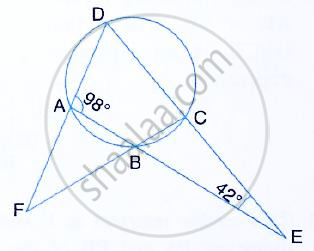
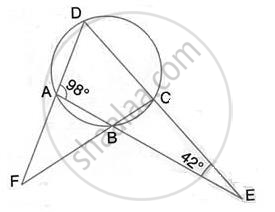
The sides AB and DC of a cyclic quadrilateral ABCD are produced to meet at E; the sides DA and CB are produced to meet at F. If ∠BEC = 42° and ∠BAD = 98°; Calculate :
(i) ∠AFB (ii) ∠ADC
Solution
By angle sum property of ∆ADE,
∠ADC = 180° - 98° - 42° = 40°
Also, ∠ADC + ∠ABC =180°
(pair of opposite angles in a cyclic quadrilateral are supplementary)
∴ ∠ABC = 180° - 40° = 140°
Also, ∠BAF = 180° - ∠BAD = 180° - 98° = 82°
∴ ∠ABC = ∠AFB + ∠BAF
(Exterior angle of a ∆ is equal to the sum of pair of interior opposite angles)
⇒ ∠AFB =140° - 82° = 58°
Thus, ∠AFB = 58° and ∠ADC = 40°
shaalaa.com
Is there an error in this question or solution?
