Question

The value of a for which the area between the curves y² = 4ax and x² = 4ay is 1 sq.unit, is ______.

Options

• `sqrt(3)`

• 4

• `4sqrt(3)`

• `sqrt(3)/4`

Answer 1

The value of a for which the area between the curves y² = 4ax and x² = 4ay is 1 sq.unit, is `underlinebb(sqrt(3)/4)`.

Explanation:

Curves is y² = 4ax and x² = 4ay.

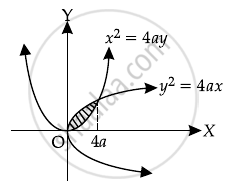
Intersection points are (0, 0) and (4a, 4a).

So, Area = `int_0^(4a)(sqrt(4ax) - x^2/(4a))dx`

Given that Area = 1

⇒ `int_0^(4a)(sqrt(4ax) - x^2/(4a))dx` = 1

⇒ `[sqrt(4a). 2/3x^(3/2) - x^3/(12a)]_0^(4a)` = 1

⇒ `2/3(4a)^2 - (4a)^3/(12a)` = 1

⇒ a = `sqrt(3)/4`