Question

The value of the integral `int_(1/3)^1 (x - x^3)^(1/3)/x^4  dx` is

Options

• 6

• 0

• 3

• 4

Answer 1

6

Explanation:

Let I = `int_(1/3)^1  (x - x^3)^(1/3)/x^4`

Put `x = sin theta, dx = cos theta  d theta`

When `x = 1/3, theta = sin^-1  1/3`, When `x = 1, theta = pi/2`

∴ I = `int_(sin^-1  1/3)^(pi/2)  (sin theta - sin^3 theta)^(1/3)/(sin^4 theta) cos theta d theta`

= `int_(sin^-1  1/3)^(pi/2) ([sin  1/3  theta(1 - sin^2 theta)]^(1/3))/theta cos theta d theta`

= `int_(sin^-1  1/3)^(pi/2) (sin theta xx cos^2 theta)^(1/3)/(sin^4 theta) cos theta d theta`

= `int_(sin^-1  1/3)^(pi/2) (sin^(1/3) theta xx cos^(2/3) theta cos theta)/(sin^4 theta) d theta`

= `int_(sin^-1  1/3)^(pi/2) (sin^(1/3) theta * cos^(5/3) theta)/(sin^2 theta sin^2 theta) d theta`

= `int_(sin^-1  1/3)^(pi/2) (cos^(5/3) theta)/(sin^(5/3) theta)  "cosec"^2theta  d theta`

= `int_(sin^-1  1/3)^(pi/2) cot^(5/3) theta  "cosec"^2 theta  d theta`

Put `cot theta = t, - "cosec"^2theta  d theta = dt`

When `theta = sin^-1  1/3` or `sin theta = 1/3, cot theta = 2sqrt(2)`

 ∴ `t = 2sqrt(2) = sqrt(8)`, When `theta = pi/2, cot theta = 0`

I = `int_sqrt(8)^0 t^(5/3) dt = int_0^sqrt(8) t^(5/3) dt`

= `3/8 (t^(8/3))_0^sqrt(8) = 3/8 (sqrt(8))^(8/3)`

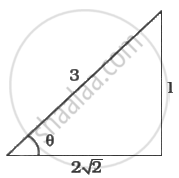
= `3/8 (8)^(8/6) = 3/8 * (8)^(4/3) = 3/8 xx 16` = 6