Question

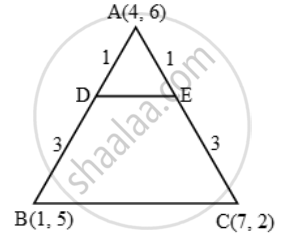
The vertices of ∆ABC = are A (4, 6), B(1, 5) and C(7, 2). A line is drawn to intersect sides AB and AC at D and E respectively such that `\frac{AD}{AB}=\frac{AE}{AC}=\frac{1}{4}` .Calculate the area of ∆ADE and compare it with the area of ∆ABC

Answer 1

We have,

`\frac{AD}{AB}=\frac{AE}{AC}=\frac{1}{4}`

`\Rightarrow \frac{AB}{AD}=\frac{AC}{AE}=4`

`\Rightarrow \frac{AD+DB}{AD}=\frac{AE+EC}{AE}=4`

`\Rightarrow 1+\frac{DB}{AD}=1+\frac{EC}{AE}=4`

`\Rightarrow \frac{DB}{AD}=\frac{EC}{AE}=3\Rightarrow\frac{AD}{DB}=\frac{AE}{EC}=\frac{1}{3}`

⇒ AD : DB = AE : EC = 1 : 3

⇒ D and E divide AB and AC respectively in the ratio 1 : 3.

So, the co-ordinates of D and E are

`( \frac{1+12}{1+3},\ \frac{5+18}{1+3} )=( \frac{13}{4},\frac{23}{4})\text{ and }( \frac{7+12}{1+3},\frac{2+18}{1+3})=( 19/ {4},\ 5)`

We have,

`∴ `

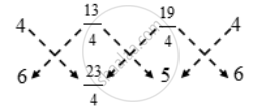
`=\frac{1}{2}|( \frac{92}{4}+\frac{65}{4}+\frac{114}{4})-( \frac{78}{4}+\frac{437}{16}+20 )|`

`=\frac{1}{2}| \frac{271}{4}-\frac{1069}{16}|`

`=\frac{1}{2}\times \frac{15}{16}=\frac{15}{32}`

Also, we have

`∴ `

`⇒ `

`⇒ Area of ∆ABC = \frac { 1 }{ 2 } |64 – 49| = `

`\therefore \frac{Area\ of\ \Delta ADE}{Area\ of\ \Delta ABC}=\frac{15/32}{15/2}=\frac{1}{16}`

Hence, Area of ∆ADE : Area of ∆ABC = 1 : 16.