Question

The volume of the greatest cylinder which can be inscribed in a cone of height 30 cm and semi-vertical angle 30° is ______.

Options

• `(4000π)/(3  cm^3)`

• `(400π)/(3  cm^3)`

• `(4000π)/(sqrt(3)  cm^3)`

• None of these

Answer 1

The volume of the greatest cylinder which can be inscribed in a cone of height 30 cm and semi-vertical angle 30° is `underlinebb((4000π)/(3  cm^3))`.

Explanation:

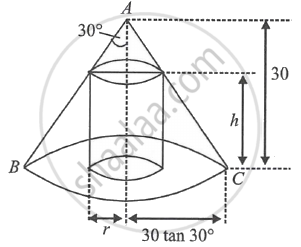
From geometry, we have `r/(30  tan 30^circ) = (30 - h)/30`

or h = `30 - sqrt(3)r`

Now, the volume of cylinder,

V = πr²h = `πr^2 (30 - sqrt(3)r)`

Now, let `(dV)/(dr)` = 0 or `π(60r - 3sqrt(3)r^2)` = 0

or r = `20/sqrt(3)`

Hence, V_max = `π(20/sqrt(3))^2 (30 - sqrt(3) 20/sqrt(3))`

= `π 400/3 xx 10`

= `(4000π)/3`