Question

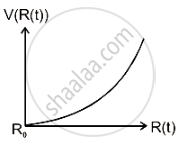
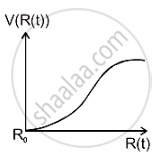
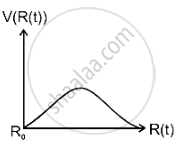
There is a uniform spherically symmetric surface charge density at a distance R_o from the origin. The charge distribution is initially at rest and starts expanding because of mutual repulsion. The figure that represents best the speed V (R(t)) of the distribution as a function of its instantaneous radius R(t) is:

Options

• 

• 

• 

• 

Answer 1

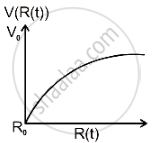
Explanation:

At any instant t, the total energy of charge distribution is constant.

U_f + K_f = U_i + K_i

i.e., `1/2"mV"^2+("KQ"^2)/(2"R") = 0+("KQ"^2)/(2"R"_0)`

∴ `1/2"mV"^2=("KQ"^2)/(2"R"_0)-("KQ"^2)/(2"R")` 

∴ V = `sqrt(2/"m""KQ"^2/2(1/"R"_0-1/"R"))`

∴ V = `sqrt("KQ"^2/"m"(1/"R"_0 -1/"R"))`

= C `sqrt(1/"R"_0-1/"R")`

In addition, the slope of the V - R curve will continue to decrease.