Advertisements
Advertisements
Question
Just as precise measurements are necessary in science, it is equally important to be able to make rough estimates of quantities using rudimentary ideas and common observations. Think of ways by which you can estimate the following (where an estimate is difficult to obtain, try to get an upper bound on the quantity):-
the wind speed during a storm
Solution 1
Wind speed during a storm can be measured by an anemometer. As wind blows, it rotates. The rotation made by the anemometer in one second gives the value of wind speed.
Solution 2
Wind speed can be estimated by floating a gas-filled balloon in air at a known height h. When there is no wind, the balloon is at A. Suppose the wind starts blowing to the right such that the balloon drifts to position B in 1 second.
Now, AB = d = hθ.
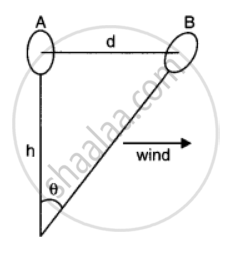
The value of d directly gives the wind speed.
APPEARS IN
RELATED QUESTIONS
How many significant figures are present in the 208?
How many significant figures should be present in the answer of the following calculation?
0.0125 + 0.7864 + 0.0215
A man walking briskly in rain with speed v must slant his umbrella forward making an angle θ with the vertical. A student derives the following relation between θ and v: tan θ = v and checks that the relation has a correct limit: as v →0, θ → 0, as expected. (We are assuming there is no strong wind and that the rain falls vertically for a stationary man). Do you think this relation can be correct? If not, guess the correct relation.
A SONAR (sound navigation and ranging) uses ultrasonic waves to detect and locate objects under water. In a submarine equipped with a SONAR the time delay between generation of a probe wave and the reception of its echo after reflection from an enemy submarine is found to be 77.0 s. What is the distance of the enemy submarine? (Speed of sound in water = 1450 m s–1).
State the number of significant figures in the following:
0.0006032 m2
Solve the numerical example.
Nuclear radius R has a dependence on the mass number (A) as R =1.3 × 10-16 A1/3 m. For a nucleus of mass number A = 125, obtain the order of magnitude of R expressed in the meter.
Solve the numerical example.
The diameter of a sphere is 2.14 cm. Calculate the volume of the sphere to the correct number of significant figures.
Answer the following question.
Describe what is meant by order of magnitude.
Write the rules for determining significant figures.
The sum of the numbers 436.32, 227.2 and 0.301 in appropriate significant figures is ______.
