Question

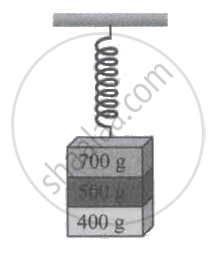
Three masses 700 g, 500 g, and 400 g are suspended at the end of a spring and are in equilibrium as shown in figure. When the 700 g mass is removed, the system oscillates with a period of 3 seconds; when the 500 g mass is also removed, it will oscillate with a period of ____________.

Options

• 1 s

• 2 s

• 3 s

• `sqrt(12/5)"s"`

Answer 1

Three masses 700 g, 500 g, and 400 g are suspended at the end of a spring and are in equilibrium as shown in figure. When the 700 g mass is removed, the system oscillates with a period of 3 seconds; when the 500 g mass is also removed, it will oscillate with a period of 2 s.

Explanation:

When mass 700 g is removed, the left out mass (500 + 400) g oscillates with a period of 3 s

`therefore 3 = "t" = 2pi sqrt((500 + 400)/"k")`    ......(i)

When 500 g mass is also removed, the left out mass is 400 g.

`therefore "t'" = 2pi sqrt(400/"k")`    ......(ii)

Dividing equation (i) by equation (ii), we get

`3/"t'" = sqrt(900/400)`

or t'= 2 s