Question

Three points masses, each of mass m are placed at the corners of an equilateral triangle of side l. The moment of inertia of the system about an axis passing through one of the vertices and parallel to the side joining other two vertices, will be ______.

Options

• `3/4 "ml"^2`

• `1/4 "ml"^2`

• `3/2 "ml"^2`

• `1/2 "ml"^2`

Answer 1

Three points masses, each of mass m are placed at the corners of an equilateral triangle of side e. The moment of inertia of the system about an axis passing through one of the vertices and parallel to the side joining other two vertices, will be `bbunderline(3/2 "ml"^2)`.

Explanation:

The given situation is as shown below,

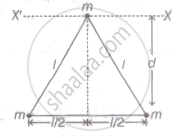
We have to find the moment of inertia about axis XX'. The distance of line XX' from base of a triangle is

d = `sqrt("i"^2 - "I"^2/4) = ((sqrt3)l)/2`

∴ Moment of inertia, due to each mass,

I = m × 0 + m`(sqrt3/2 "l")^2 + "m"(sqrt3/2 "l")^2`

`= (3 "ml"^2)/4 + (3 "ml"^2)/4`

= `(6 "ml"^2)/4`

= `(3 "ml"^2)/2`

OR

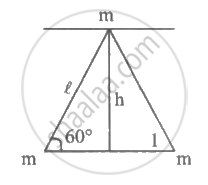
I = 2mh²

`h=lsin60^circ=lxxsqrt3/2`

`"I"=2mxx3/4*l^2=3/2ml^2`