Advertisements
Advertisements
Question
Three of the six vertices of a regular hexagon are chosen at random. What is the probability that the triangle with these vertices is equilateral.
Solution
We choose three vertices out of 6 in 6C3 = 20 ways.
∴ Total number of elementary events = n(S) = 20
Number of ways of choosing an equilateral triangle = 2
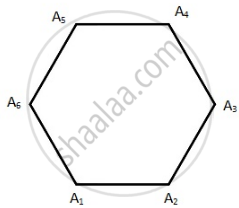
i.e. A1A3A5 or A2A4A6
∴ Total number of favourable events = n(E) = 2
Hence, required probability = \[\frac{2}{20} = \frac{1}{10}\]
APPEARS IN
RELATED QUESTIONS
Describe the sample space for the indicated experiment: A coin is tossed four times.
A box contains 1 red and 3 identical white balls. Two balls are drawn at random in succession without replacement. Write the sample space for this experiment.
If a coin is tossed three times (or three coins are tossed together), then describe the sample space for this experiment.
Write the sample space for the experiment of tossing a coin four times.
What is the total number of elementary events associated to the random experiment of throwing three dice together?
A coin is tossed repeatedly until a tail comes up for the first time. Write the sample space for this experiment.
A coin is tossed twice. If the second draw results in a head, a die is rolled. Write the sample space for this experiment.
A bag contains 4 identical red balls and 3 identical black balls. The experiment consists of drawing one ball, then putting it into the bag and again drawing a ball. What are the possible outcomes of the experiment?
An experiment consists of boy-girl composition of families with 2 children.
What is the sample space if we are interested in knowing whether it is a boy or girl in the order of their births?
An experiment consists of rolling a die and then tossing a coin once if the number on the die is even. If the number on the die is odd, the coin is tossed twice. Write the sample space for this experiment.
A die is thrown repeatedly until a six comes up. What is the sample space for this experiment.
Three coins are tossed once. Describe the events associated with this random experiment:
A = Getting three heads
B = Getting two heads and one tail
C = Getting three tails
D = Getting a head on the first coin.
(iii) Which events are compound events?
A card is drawn at random from a pack of 52 cards. Find the probability that the card drawn is black and a king
A card is drawn at random from a pack of 52 cards. Find the probability that the card drawn is a jack, queen or a king
A card is drawn at random from a pack of 52 cards. Find the probability that the card drawn is a diamond card
A bag contains 7 white, 5 black and 4 red balls. If two balls are drawn at random, find the probability that both the balls are white
Five cards are drawn from a pack of 52 cards. What is the chance that these 5 will contain:
(i) just one ace
The face cards are removed from a full pack. Out of the remaining 40 cards, 4 are drawn at random. what is the probability that they belong to different suits?
There are four men and six women on the city councils. If one council member is selected for a committee at random, how likely is that it is a women?
Find the probability that in a random arrangement of the letters of the word 'UNIVERSITY', the two I's do not come together.
Two balls are drawn at random from a bag containing 2 white, 3 red, 5 green and 4 black balls, one by one without, replacement. Find the probability that both the balls are of different colours.
20 cards are numbered from 1 to 20. One card is drawn at random. What is the probability that the number on the cards is not a multiple of 4?
20 cards are numbered from 1 to 20. One card is drawn at random. What is the probability that the number on the cards is divisible by 5?
A class consists of 10 boys and 8 girls. Three students are selected at random. What is the probability that the selected group has all girls?
A class consists of 10 boys and 8 girls. Three students are selected at random. What is the probability that the selected group has at most one girl?
A bag contains tickets numbered from 1 to 20. Two tickets are drawn. Find the probability that both the tickets have prime numbers on them
An urn contains 7 white, 5 black and 3 red balls. Two balls are drawn at random. Find the probability that both the balls are red .
An urn contains 7 white, 5 black and 3 red balls. Two balls are drawn at random. Find the probability that one ball is white.
An integer is chosen at random from first 200 positive integers. Find the probability that the integer is divisible by 6 or 8.
Suppose an integer from 1 through 1000 is chosen at random, find the probability that the integer is a multiple of 2 or a multiple of 9.
Two dice are thrown together. The probability that at least one will show its digit greater than 3 is
Four persons are selected at random out of 3 men, 2 women and 4 children. The probability that there are exactly 2 children in the selection is
A typical PIN (personal identification number) is a sequence of any four symbols chosen from the 26 letters in the alphabet and the ten digits. If all PINs are equally likely, what is the probability that a randomly chosen PIN contains a repeated symbol?
If 10 different balls are to be placed in 4 distinct boxes at random, then the probability that two of these boxes contain exactly 2 and 3 balls is ______.
