Question

Trace the rays of light showing the formation of an image due to a point object placed on the axis of a spherical surface separating the two media of refractive indices n₁ and n₂. Establish the relation between the distances of the object, the image and the radius of curvature from the central point of the spherical surface.

Hence derive the expression of the lens maker’s formula.

Answer 1

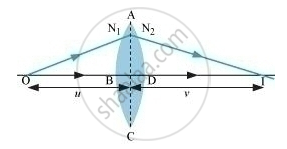
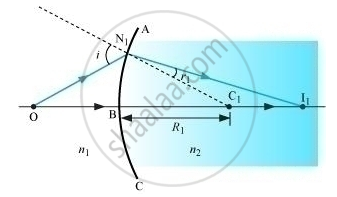
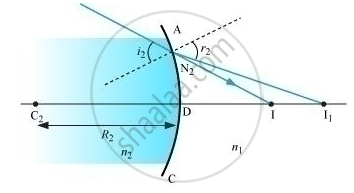
In the given figure, image is I and object is denoted as O.

The centre of curvature is C.

The rays are incident from a medium of refractive index `n_1`to another of refractive index`n_2`.

We consider NM to be perpendicular to the principal axis.

`tan angleNOM = (MN)/(OM)`

`tan angleNCM = (MN)/(MC)`

`tan angleNIM = (MN)/(MI)`

For ΔNOC, i is the exterior angle.

Therefore, i = ∠NOM + ∠NCM

`i =(MN)/(OM) + (MN)/(MC)`

Similarly,

r = ∠NCM − ∠NIM

i.e., `r = (MN)/(MC) - (MN)/(MI)`

According to Snell’s law,

`n_1 sin i = n_2 sin r`

For small angles,

`n_1i = n_2r`

Substituting i and r, we obtain

`n_1/(OM) + (n_2)/(MI) = (n_2 - n_1)/(MC)`

Where, OM, MI, and MC are the distances

OM = −u

MC = +R

MI = v

Substituting these, we obtain

`n_2/v -n_1/u = (n_2 -n_1)/R     ..  (1)`

Applying equation (i) to lens ABCD, we obtain for surface ABC,

`n_1 /(OB) +n_2/(BI_1) = (n_2 -n_1)/(BC_1)    ... (2)`

For surface ADC, we obtain
`(-n_2)/(DI_1) + (n_1)/(DI) = (n_2n_1)/(DC_2) ..... (3)`

For a thin lens,

BI₁ = DI₁­

Adding (ii) and (iii), we obtain

`n_1/(OB) + n_1/(DI) = (n_2-n_1) [1/(BC_1) +1/(DC_2)]`

Suppose object is at infinity and DI = f, then

`n_1/f = (n_2 - n_1) [1/(BC_1)+1/(DC_2)]`

This is known as lens maker’s formula.