Question

Two blocks each of mass m lie on a smooth table. They are attached to two other masses as shown in the figure. The pulleys and strings are light. An object O is kept at rest on the table. The sides AB and CD of the two blocks are plane and made reflecting. The acceleration of two images formed in those two reflecting surfaces with respect to each other is ______.

 

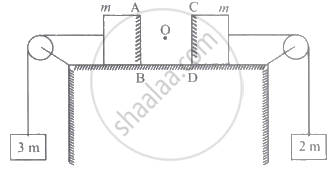
Options

• `(13g)/6`

• `(11g)/6`

• `(17g)/6`

• `(19g)/6`

Answer 1

Two blocks each of mass m lie on a smooth table. They are attached to two other masses as shown in the figure. The pulleys and strings are light. An object O is kept at rest on the table. The sides AB and CD of the two blocks are plane and made reflecting. The acceleration of two images formed in those two reflecting surfaces with respect to each other is `underlinebb((17g)/6).`

Explanation:

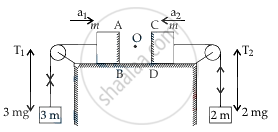
Let the acceleration of AB is a₁ and the acceleration of CO be a₂.

For AB

3mg - T₁ = 3ma₁ ..........(i)

T₁ = ma₁ ............(ii)

From (i) and (ii),

3mg = 4ma₁

⇒ `a_1 = (3mg)/(4m)`

⇒ `a_1 = (3g)/4`

For CD

2mg - T₂ = 2ma₂ .................(iii)

T₂ = ma₂ ................(iv)

From equation (iii) and (iv),

2mg = 3ma₂

⇒ `a_2 = (2mg)/(3m)`

⇒ `a_2 = (2g)/3`

Now, acceleration of image in AB mirror.

`(a_{AB}) = 2a_1`

= `2 xx (3g)/4`

= `(3g)/2`

Acceleration of image in mirror CD.

`(a_{CD}) = 2a_2`

= `2 xx (2g)/3`

= `(4g)/3`

So, relative acceleration = a₁ + a₂

= `(3g)/2 + (4g)/3`

= `(9g + 8g)/6`

= `(17g)/6`