Advertisements
Advertisements
Question
Two charged particles traverse identical helical paths in a completely opposite sense in a uniform magnetic field B = B0k̂.
Options
They have equal z-components of momenta.
They must have equal charges.
They necessarily represent a particle-antiparticle pair.
The charge to mass ratio satisfy : `(e/m)_1 + (e/m)_2 = 0`.
Solution
The charge to mass ratio satisfy : `(e/m)_1 + (e/m)_2 = 0`.
Explanation:
In this situation, if the particle is thrown in x - y plane (as shown in figure) at some angle θ with velocity v, then we have to resolve the velocity of the particle in rectangular components, such that one component is along the field (v cosθ) and another one is perpendicular to the field (v sinθ). We find that the particle moves with constant velocity v cosθ along the field. The distance covered by the particle along the magnetic field is called pitch.
The pitch of the helix, (i.e., linear distance travelled in one rotation) will be given by
`p = T(v cos theta) = 2p m/(qB) (v cos theta)`
For given pitch p correspond to charge particle, we ahve
`q/m = (2pi v cos theta)/(qB)` = constant
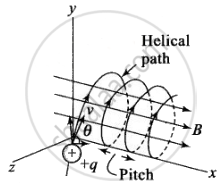
Here in this case, charged particles traverse identical helical paths in a completely opposite sense in a uniform magnetic field B, LHS for two particles should be the same and of opposite sign. Therefore, `(e/m)_1 + (e/m)_2 = 0`
APPEARS IN
RELATED QUESTIONS
A rod of length l is moved horizontally with a uniform velocity 'v' in a direction perpendicular to its length through a region in which a uniform magnetic field is acting vertically downward. Derive the expression for the emf induced across the ends of the rod.
A particle of charge ‘q’ and mass ‘m’ is moving with velocity .`vecV` It is subjected to a uniform magnetic field `vecB` directed perpendicular to its velocity. Show that it describes a circular path. Write the expression for its radius.
The net charge in a current-carrying wire is zero. Then, why does a magnetic field exert a force on it?
What is Lorentz force?
A deuteron of kinetic energy 50 keV is describing a circular orbit of radius 0.5 metre in a plane perpendicular to the magnetic field B. The kinetic energy of the proton that describes a circular orbit of radius 0.5 metre in the same plane with the same B is ______.
- If v is parallel to B, then path of particle is spiral.
- If v is perpendicular to B, then path of particle is a circle.
- If v has a component along B, then path of particle is helical.
- If v is along B, then path of particle is a circle.
The correct plot of the magnitude of magnetic field `vec"B"` vs distance r from centre of the wire is, if the radius of wire is R.
A charge particle moves along circular path in a uniform magnetic field in a cyclotron. The kinetic energy of the charge particle increases to 4 times its initial value. What will be the ratio of new radius to the original radius of circular path of the charge particle:
Two long parallel current-carrying conductors are 0.4 m apart in air and carry currents 5 A and 10 A. Calculate the force per metre on each conductor, if the currents are (a) in the same direction and (b) in the opposite direction.
