Question

Two cylinders A and B of the same material have same length, their radii being in the ratio 1 : 2 respectively. The two are joined end to end as shown in the figure. One end of cylinder A is rigidly clamped while free end of cylinder B is twisted through an angle θ. The angle of twist of cylinder A is ______.

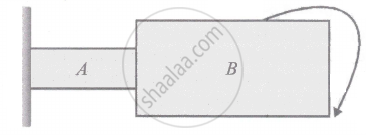
Options

• `17/16 theta`

• 16 θ

• 17 θ

• `16/17 theta`

Answer 1

Two cylinders A and B of the same material have same length, their radii being in the ratio 1 : 2 respectively. The two are joined end to end as shown in the figure. One end of cylinder A is rigidly clamped while free end of cylinder B is twisted through an angle θ. The angle of twist of cylinder A is `underline(16/17 theta)`.

Explanation:

Torque required to produce unit twist

T = `(pi"nr")^4/l theta`

`"T"_"A"/"T"_"B" = (("r"_"A")^4 theta_"A")("r"_"B"^4 theta_"B")` or, `theta_"A"/theta_"B" = ("r"_"B")^2/("r"_"A")^2 = (4"r")^2/("r"^2)` = 16

`therefore theta"A" = 16  theta_"B" = theta_"A"/16`

And according to question, `theta = theta_"A" + theta_"B"`

or, θ = `theta_"A" + theta_"A"/16 = 17/16 theta_"A"`

`therefore theta_"A" = 16/17 theta`