Question

Two heavy spheres each of mass 100 kg and radius 0.10 m are placed 1.0 m apart on a horizontal table. What is the gravitational force and potential at the mid point of the line joining the centers of the spheres? Is an object placed at that point in equilibrium? If so, is the equilibrium stable or unstable?

Answer 1

0;

–2.7 × 10^–8 J /kg;

Yes;

Unstable

Explanation:

The situation is represented in the given figure:

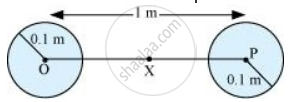
Mass of each sphere, M = 100 kg

Separation between the spheres, r = 1m

X is the mid point between the spheres. Gravitational force at point X will be zero. This is because gravitational force exerted by each sphere will act in opposite directions.

Gravitational potential at point X:

`=(-GM)/((r/2)) - (GM)/((r/2)) = -4(GM)/r`

`=(4xx6.67xx10^(-11)xx100)/1`

`=-2.67xx10^(-8) J/Kg`

Any object placed at point X will be in equilibrium state, but the equilibrium is unstable. This is because any change in the position of the object will change the effective force in that direction.

Answer 2

Here G = 6.67 x 10^-11 Nm² kg^-2; M = 100 kg; R = 0.1 m, distance between the two spheres, d = 1.0 m
Suppose that the distance of either sphere from the mid-point of the line joining their centre is r. Then r=d/2=0.5 m. The gravitational field at the mid-point due to two spheres will be equal and opposite.

Hence the resultant gravitational field at the mid poiint  = 0

The gravitational potential at the mid point = `(-"GM"/r)xx2`

= `-(6.67xx10^(-11)xx 100 xx 2)/0.5 = -2.668xx10^(-8) J kg^(-1)`

The object placed at that point would be in stable equilibrium.