Advertisements
Advertisements
Question
Two identical resistros of `12 Omega` each are connected to a battery of 3V . Calculate the ratio of the power consumed by the resulting combinations with minimum resistance and maximum resistance.
Solution
`R_1 = 12 Omega`
`R_2 = 12 Omega`
`V = 3 V`
Minimum resistance ⇒ Parallel combination.
`1/R = 1/R_1 + 1/R_2`
= `12.12/(12 + 12) = 6 Omega`
`6 Omega` = minimum resistance
`therefore P = V^2/R = (3)^2/((6)) = 9/6 = 3/2 = 1.5 "watt"`
for maximum resistance
`R = R_1 + R_2 = 12 + 12 = 24 Omega`
`therefore P_(min) = V^2/R = (3)^2/24 = 9/24 = 3/8 "watt"`
`P_(min)/P_(max) = 3/8 = 1/4`
APPEARS IN
RELATED QUESTIONS
Three resistors of resistances R1 , R2 and R3 are connected (i) in series, and (ii) in parallel. Write expressions for the equivalent resistance of the combination in each case.
Water can conduct electricity.
A cell, a resistor, a key and ammeter are arranged as shown in the circuit diagrams of Figure. The current recorded in the ammeter will be
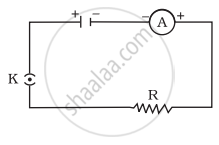 |
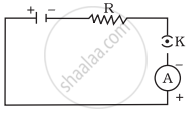 |
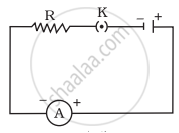 |
| (i) | (ii) | (iii) |
Electrical resistivity of a given metallic wire depends upon
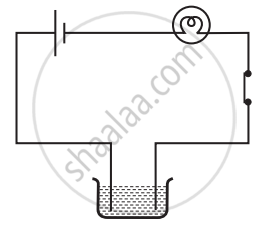
Boojho made the circuit given in the figure and observed that the bulb did not glow. On Paheli’s suggestion, he added one more cell in the circuit. The bulb now glows. Explain.
Which of the following precautions need not be taken while using electric gadgets/appliances/circuits?
Why are compact fluorescent lamps (CFLs) preferred over electric bulbs?
Why is an electric fuse required in all electrical appliances?
Electricity produced on rubbing is ______.
In an electric bulb, light is produced due to the glowing of
