Question

Two kinds of foods A and B are being considered to form a weekly diet. The minimum weekly requirements of fats, Carbohydrates and proteins are 12, 16 and 15 units respectively. One kg of food A has 2, 8 and 5 units respectively of these ingredients and one kg of food B has 6, 2 and 3 units respectively. The price of food A is Rs. 4 per kg and that of food B is Rs. 3 per kg. Formulate the L.P.P. and find the minimum cost.

Answer 1

Let x kg of food A and y kg of food B be purchased.

Ingredients/foods	A (x)	B (y)	Minimum requirement
Fats	2	6	12
Carbohydrates	8	2	16
Proteins	5	3	15

The L.P.P. is

Minimize Z = 4x + 3y,

Subject to 2x + 6y ≥ 12,

8x + 2y ≥ 16,

5x + 3y ≥ 15,

x ≥ 0, y ≥ 0

To draw	x	y	(x, y)	Sign	Region lies on
L1: 2x + 6y = 12	0	2	A(0, 2)	≥	Non-origin side of line L1
	6	0	B(6, 0)
L2: 8x + 2y = 16	0	8	C(0, 8)	≥	Non-origin side of line L2
	2	0	D(2, 0)
L3: 5x + 3y = 15	0	5	E(0, 5)	≥	Non-origin side of line L3
	3	0	F(3, 0)

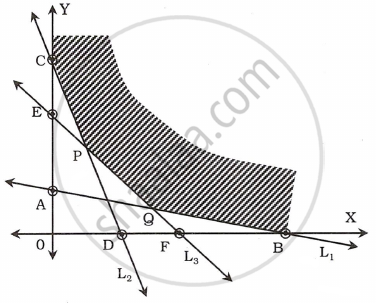
Solving equations of L₂ and L₃

    4x + y = 8
  5x + 3y = 15
12x + 3y = 24
  5x + 3y = 15
–     –      –      
  7x        =   9

∴ x = `9/7`, y = `20/7`

∴ P = `(9/7, 20/7)`

Solving equations of L₁ and L₃

    x + 3y =  6
  5x + 3y = 15
–     –        –     
  –4x      = –9

∴ x = `9/7`, y = `5/7`

∴ Q = `(9/7, 5/7)`

∴ The feasible region is CPQB

Vertices	Value of Z = 4x + 3y
C(0, 8)	24
`P(9/7, 20/7)`	`36/7 + 60/7` = 13.7
`Q(9/4, 5/4)`	`36/4 + 15/4` = 12.7
B(6, 0)	24

∴  Z is minimum at x = `9/7`, y = `5/4` and Min. Z = 12.7