Question

Two mercury droplets of radii 0.1 cm. and 0.2 cm. collapse into one single drop. What amount of energy is released? The surface tension of mercury T = 435.5 × 10^–3 Nm^–1.

Answer 1

When two drops form a bigger drop, volume remains conserved.

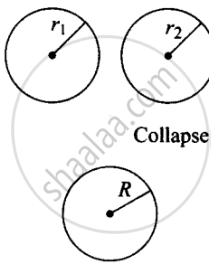
According to the problem, there is two mercury droplets of different radii collapse into one single drop.

Radius of smaller drop = r₁ = 0.1 cm = 10^–3 m

Radius of bigger drop = r₂ = 0.2 cm = 2 × 10^–3 m

Surface tension (T) = 435.5 × 10^–3 N/m

Let V₁ and V₂ be the volumes of these two mercury droplets and the volume of big drops formed by collapsing is V.

The volume of a big drop = Volume of small droplets

`V = V_1 6 V_2`

`4/3 πR^3 = 4/3 πr_1^3 + 4/3 πr_2^3`

or `R^3 = r_1^3 + r_2^3`

= (0.1)³ + (0.2)³

= 0.001 + 0.008 

= 0.009

or R = 0.21 cm = 2 × 10^–3 m

∴ Decrease in surface area,

ΔA = `4πR^2 - (4πr_1^2 + 4πr_2^2)`

= `4π[R^2 - (r_1^2 + r_2^2)]`

Energy released,

`E = T xx ΔA`

= `T xx 4π[R^2 - (r_1^2 + r_2^2)]`

= `435.5 xx 10^-3 xx 4 xx 3.14[(2.1 xx 10^-3)^2 - (1 xx 10^-6 + 4 xx 10^-6)]`

= `435.5 xx 4 xx 3.14[4.41 - 5] xx 10^-6 xx 10^-3`

= – 32.23 × 10^–7 ......(Negative sign shows absorption)

Therefore, 3.22 × K^–6 J energy will be absorbed. So, the surface area of the water decreases means the surface area of bigger drop is less than the sum of surface area of two smaller drops.