Question

Two parallel chords are drawn in a circle of diameter 30.0 cm. The length of one chord is 24.0 cm and the distance between the two chords is 21.0 cm; find the length of another chord.

Answer 1

Since the distance between the chords is greater than the radius of the circle (15 cm), so the
chords will be on the opposite sides of the centre.

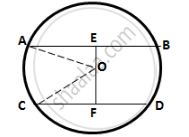
Let O be the centre of the circle and AB and CD be the two parallel chords such that
AB = 24 cm.
Let length of CD be 2x cm.
Drop OE and OF perpendicular on AB and CD from the centre O.
OE ⊥ AB and OF⊥CD
∴ OE bisects AB and OF bisects CD
(Perpendicular drawn from the centre of a circle to a chord bisects it)

⇒ AE = `24/2` = 12cm; CF = `(2x)/2` =x cm

In right ΔOAE,

OA² = OE²+AE²

⇒ OE² = OA² - AE² = (15)² - (12)² = 81

∴ OE = 9 cm
∴ OF = EF - OE = (21- 9) =12 cm

In right ΔOCF,

OC² = OF² + CF²

⇒ x² = OC² - OF² = (15)² -   (12)² = 81
∴ x = 9 cm
Hence, length of chord CD = 2x = 2×9 =18 cm