Question

Two particles of equal mass 'm' go around a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle with respect to its centre of mass is ______.

Options

• `sqrt((Gm)/(4R))`

• `sqrt((Gm)/(3R))`

• `sqrt((Gm)/(2R))`

• `sqrt((Gm)/(R))`

Answer 1

Two particles of equal mass 'm' go around a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle with respect to its centre of mass is `underlinebb(sqrt((Gm)/(4R)))`.

Explanation:

As two masses revolve about the common centre of mass O.

 

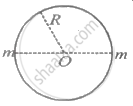
∴ Mutual gravitational attraction = centripetal force

`(Gm^2)/(2R)^2 = momega^2R`

⇒ `(Gm)/(4R^3) = omega^2`

⇒ `omega = sqrt((Gm)/(4R^3))`

If the velocity of the two particles with respect to the centre of gravity is v. then,

v = ωR

v = `sqrt((Gm)/(4R^3)) xx R = sqrt((Gm)/(4R))`