Question

Two point charges Q each are placed at a distance d apart. A third point charge q is placed at a distance x from the mid-point on the perpendicular bisector. The value of x at which charge q will experience the maximum Coulomb's force is ______.

Options

• x = d

• `x = d/2`

• `x = d/sqrt2`

• `x = d/(2sqrt2)`

Answer 1

Two point charges Q each are placed at a distance d apart. A third point charge q is placed at a distance x from the mid-point on the perpendicular bisector. The value of x at which charge q will experience the maximum Coulomb's force is `bbunderline(x = d/(2sqrt2))`.

Explanation:

According to the given condition, we have:

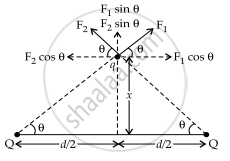
We can infer from the diagram that the net electric force will be 2F sinθ in the vertical direction.

Hence, `F_"net" = 2F sintheta`

`sintheta = "x"/sqrt(d^2/4 + x^2)`

`F_"net" = 2 xx 1/(4piε_0) xx (Q_x)/(d^2/4 + x^2)^{3"/"2}`

For F_net to be maximum, `d/dx F_"net" = 0`

⇒ `d/dx[2 xx 1/(4piε_0) xx (qQx)/(d^2/4 + x^2)^{3"/"2}] = 0`

⇒ `(d^2/4 + x^2)^{-3"/"2} (d(x))/(dx) + x d/dx(d^2/4 + x^2)^{-3"/"2} = 0`

⇒ `(d^2/4 + x^2)^{-3"/"2} + ((-3)/2)(d^2/4 + x^2)^{-5"/"2}(2x) = 0`

⇒ `1/(d^2/4 + x^2)^{3"/"2} = (3x^2)/(d^2/4 + x^2)^{5"/"2}`

⇒ `d^2/4 + x^2 = 3x^2`

⇒ `d^2/4 = 2x^2`

⇒ `d^2 = 8x^2`

⇒ `x^2 = d^2/8`

Hence, `x = d/(2sqrt2)`