Question

Two spherical mirrors, one convex and the other concave, each of same radius of curvature R are arranged coaxially at a distance of 2R from each other. A small circle of radius a is drawn on the convex mirror as shown in figure. What is the radii of first two images of the circle?

 

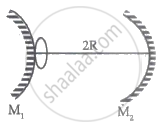
Options

• `a/3, a/11`

• `a/6, a/2`

• `a/3, a/4`

• `a/12, a/4`

Answer 1

`underlinebb(a/3, a/11)`

Explanation:

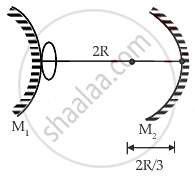
When the first reflection occurs on a concave mirror and the second on a convex mirror,

For concave: `u = -2R, f = (-R)/2`

`1/v + 1/u = 1/f`

⇒ `1/v + 1/(-2R) = (-2)/R`

`1/v = (-2)/R + 1/(2R)`

⇒ `v = (-2R)/3`

m = `-v/u`

= `-(((-2R)/3)/(2R)) = (-1)/3`

Size of image = `-a/3` (laterally inverted)

For convex:

`u = (-4R)/3, f = R/2`

`1/v + 1/u = 1/f`

⇒ `1/v = 2/R + 3/(4R)`

`v = +(4R)/11`

m = `-v/u = -(((-4R)/11)/((4R)/3)) = 3/11`

Size of image = `3/11 a/3 = a/11`