Question

Two vertical poles are 150 m apart and the height of one is three times that of the other. If from the middle point of the line joining their feet, an observer finds the angles of elevation of their tops to be complementary, then the height of the shorter pole (in meters) is ______.

Options

• 25

• `20sqrt(3)`

• 30

• `25sqrt(3)`

Answer 1

Two vertical poles are 150 m apart and the height of one is three times that of the other. If from the middle point of the line joining their feet, an observer finds the angles of elevation of their tops to be complementary, then the height of the shorter pole (in meters) is `underlinebb(25sqrt(3))`.

Explanation:

Given: Let AB and PQ be poles 150m apart.

Height of AB is 3 times that of PQ.

Let the midpoint of BQ is M.

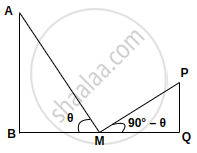
Let ∠AMB = θ

∴ ∠PMQ = 90° – θ  ...(∵ Both angles are complementary)

Let AB = h, PQ = `"h"/3`, BM = x, QM = x

In ΔAMB, tanθ = `"h"/x`  ...(i)

In ΔPMQ, tan(90° – θ) = `("h"/3)/x`

⇒ cotθ = `"h"/(3x)`  ...(ii)

Multiply equation (i) and equation (ii)

`"h"/x xx "h"/(3x)` = 1

⇒ h² = 3x²

⇒ h = `sqrt(3)x`

Given, 2x = 150 ⇒ x = 75

∴ h = `75sqrt(3)`

Height of shorter pole = `"h"/3 = 25sqrt(3)"m"`