Advertisements
Advertisements
Question
Using integration, find the area of the region bounded by the line y – 1 = x, the x-axis and the ordinates x = – 2, x = 3
Solution
The equation of given line is y – 1 = x
y = x + 1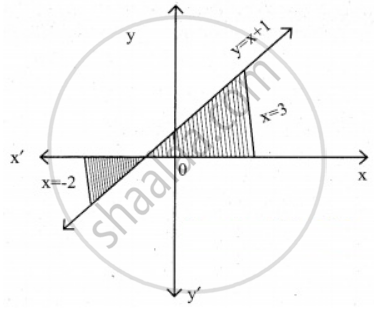
The line y = x + 1 meets the x-axis at x = – 1
Since x varies from – 2 to 3
Hence a part of lies below the x-axis and the other part lies above the x-axis.
∴ Area A = `int_(-2)^(-1) (- y) "d"x + int_(-1)^3 y "d"x`
= `int_(-2)^(-1) (x + 1) "d"x + int_(-1)^3 (x + 1) "d"x`
= `- [x^2/2 + x]_(-2)^(-1) + [x^2/2 + x]_(-1)^3`
= `{[(-1)^2/2 + (-1)] - [(-2)^2/2 + (-2)]} + {[(3)^2/2 + (3)] - [(-1)^2/2 + (-1)]}`
= `{(1/2 - 1) - (4/2 - 2)} + {(9/2 + 3) - (1/2 - 1)}`
= `- {(-1)/2 - 0} + 0 + {9/2 + 3 + 1/2}`
= `1/2 + 9/2 + 3 + 1/2`
= `(1 + 9 + 6 + 1)/2`
A = `17/2` sq.units
APPEARS IN
RELATED QUESTIONS
Find the area bounded by the lines y – 2x – 4 = 0, y = 0, y = 3 and the y-axis
Find the area bounded by the curve y = x2 and the line y = 4.
Choose the correct alternative:
Area bounded by the curve y = x(4 – x) between the limits 0 and 4 with x-axis is
Choose the correct alternative:
Area bounded by the curve y = e–2x between the limits 0 ≤ x ≤ `oo` is
Choose the correct alternative:
Area bounded by the curve y = `1/x` between the limits 1 and 2 is
Choose the correct alternative:
Area bounded by y = ex between the limits 0 to 1 is
Choose the correct alternative:
The area bounded by the parabola y2 = 4x bounded by its latus rectum is
Choose the correct alternative:
Area bounded by y = |x| between the limits 0 and 2 is
Find the area of the region bounded by the curve between the parabola y = 8x2 – 4x + 6 the y-axis and the ordinate at x = 2
Find the area of the region bounded by the curve y2 = 27x3 and the lines x = 0, y = 1 and y = 2
