Question

Using the factor Theorem, show that:

2x + 7 is a factor 2x³ + 5x² − 11x – 14. Hence, factorise the given expression completely.

Answer 1

f(x) = 2x³ + 5x² - 11x - 14

2x + 7 = 0  ⇒  x = `((-7)/2)`

Remainder = `f((-7)/2)`

`= 2((-7)/2)+5((-7)/2)^2-11((-7)/2)-14`

= `(-343)/4 + 245/4 + 77/2 - 14`

= `(-49)/2 + 77/2 -14`

= `28/2 -14`

= 14 - 14 = 0

Hence, (2x + 7) is a factor of f(x).
Now, we have:

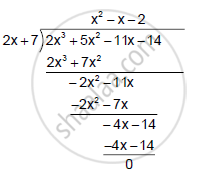
∴ `2x^3+5x^2-11x-14 = (2x + 7) (x^2- x-2)`

= `(2x +  7)(x^2 - 2x + x -2 )`

= `(2x + 7 )[x(x-2)+(x-2)]`

= `(2x + 7)(x-2)(x+1)`