Question

Using vector method, prove that the perpendicular bisectors of sides of a triangle are concurrent.

Answer 1

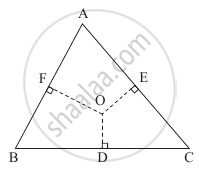
Let D, E, F be the midpoints of the sides BC, CA and AB of ΔABC.

Let the perpendicular bisectors of the sides BC and AC meet each other in the point O.

Choose O as the origin and let `bara, barb, barc, bard, bare` and `barf` be the position vectors of the points A, B, C, D, E, F respectively.

Here, we have to prove that `bar(OF) = barf` is perpendicular to `bar(AB) = barb - bara`.

By the midpoint formula

`bard = (barb +  barc)/2, bare = (barc + bara)/2, barf = (bara + barb)/2`

Now, `bar(OD) = bard` is perpendicular to `bar(BC) = barc - barb` 

∴ `bard*(barc - barb)` = 0

∴ `(barb + barc)/2*(barc - barb)` = 0

∴ `(barc + barb)*(barc - barb)` = 0

∴ `barc*barc + barb*barc - barc*barb - barb*barb` = 0

∴ c² – b² = 0   ...`[∵ barc*barc = c^2, barb*barb = b^2 and barc*barb = barb*barc]`

∴ c² = b²    ...(1)

Also, `bar(OE) = bare` is perpendicular to `bar(AC) = barc - bara`

∴ `bare*(barc - bara)` = 0

∴ `(barc + bara)/2*(barc - bara)` = 0

∴ As above c² = a²    ...(2)

∴ From (1) and (2), we get

b² = a²

∴ b² – a² = 0

∴ `(barb + bara)*(barb - bara)` = 0

∴ `(barb + bara)/2*(barb - bara)` = 0

∴ `barf*(barb - bara)` = 0

∴ `barf = bar(OF)` is perpendicular to `barb - bara = bar(AB)`

Hence, the perpendicular bisectors of the sides of ΔABC are concurrent.