Advertisements
Advertisements
Question
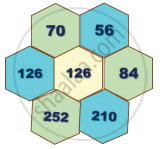
Verify whether the following hexagonal shapes form a part of the Pascal’s Triangle.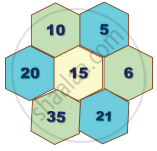
Solution
In Pascal’s Triangle product of the 3 alternate numbers given around the hexagon is equal to the product of remaining three numbers.

5 × 21 × 20 = 10 × 6 × 35 = 2100
∴ It form a part of Pascal’s Triangle
APPEARS IN
RELATED QUESTIONS
Complete the Pascal’s Triangle by taking the numbers 1, 2, 6, 20 as line of symmetry.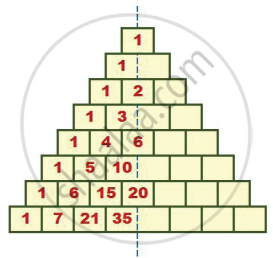
The elements along the sixth row of the Pascal’s Triangle is
What is the sum of the elements of nineth row in the Pascal’s Triangle?
Find the triangular numbers from the Pascal’s Triangle and colour them.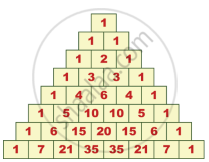
Write the first five numbers in the third slanting row of the Pascal’s Triangle and find their squares. What do you infer?
The following hexagonal shapes are taken from Pascal’s Triangle. Fill in the missing numbers.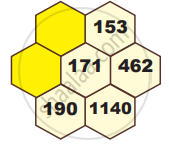
The following hexagonal shapes are taken from Pascal’s Triangle. Fill in the missing numbers.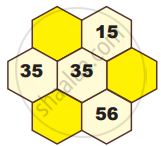
Verify whether the following hexagonal shapes form a part of the Pascal’s Triangle.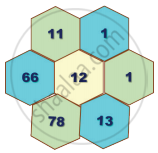
Verify whether the following hexagonal shapes form a part of the Pascal’s Triangle.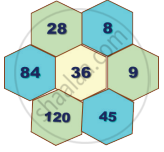
Verify whether the following hexagonal shapes form a part of the Pascal’s Triangle.